Stabilität und Instabilität in Flüssigkeiten und Materialien

In der Forschungsgruppen beschäftigen wir uns mit physikalisch motivierten Problemen in den partiellen Differentialgleichungen.
Insbesondere interessieren wir uns für Durchmischungs- und Resonanzeffekte in Strömungsgleichungen mit und ohne Dissipation und für Rigidität und Flexibilität in der variationellen Beschreibung von Formgedächtnismaterialien.

Durchmischung und (In)Stabilität

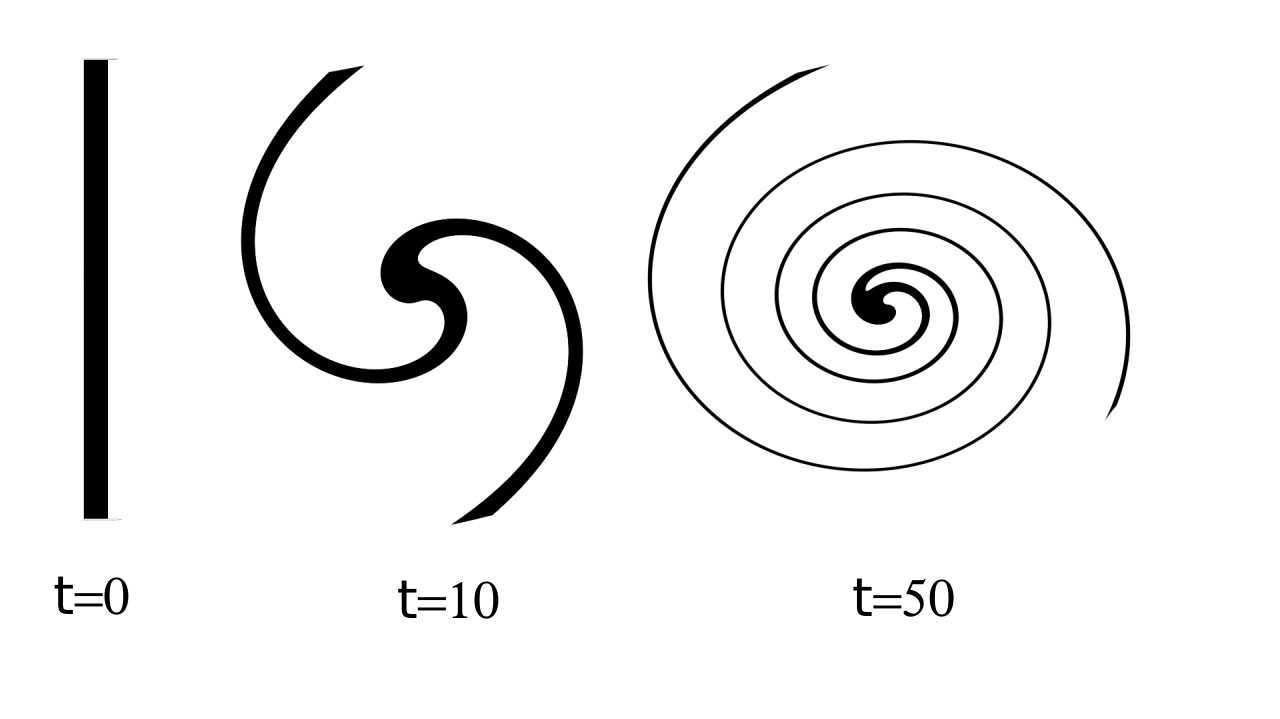
Mixed

Eine zentrale Frage der Strömungslehre ist die Beschreibung der Stabilität und des Langzeitverhaltens von Fluiden (Flüssigkeiten oder Gase).
Hierbei interessieren wir uns insbesondere für Lösungen der inkompressiblen Euler Gleichungen

$\partial_t v + v \cdot \nabla v - \nabla p = 0,$
$\text{div}(v)=0,$

welche die Evolution eines Fluids mittels eines Geschwindigkeitsvektofeldes $v$ und des Drucks $p$ beschreiben.
Im Gegensatz zu den Navier-Stokes oder Boltzmann Gleichungen beinhalten die Euler Gleichungen keine üblichen Dämpfungsmechanismen wie Dissipation oder Entropiezunahme.
Es ist daher eine zunächst sehr überraschende Beobachtung, dass Störungen um bestimmte Scherströmungen $v=(U(y),0)$ im Laufe der Zeit wieder zu Scherströmungen konvergieren -- Ein als "invicid damping" bekanntes Phänomen.
Mathematisch führt dies zu Fragen zu schwacher Konvergenz, Durchmischung und einerseits Dämpfung von Störungen (in negativen Sobolev Normen) aber andererseits zu wachsender Irregularität und feinen Durchmischungsskalen.
Diese Durchmischungseffekte und ihre Auswirkungen auf nichtlineare Instabilität sind ein zentraler Gegenstand unserer Forschung.

Resonanzkaskaden in gekoppelten Systemen

Resonanz

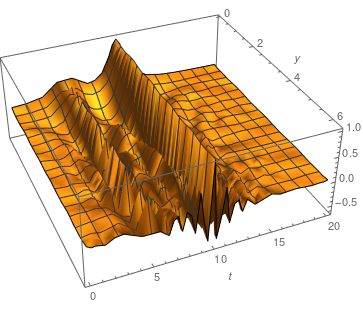
In gekoppelten Fluid Systeme wie den Boussinesq Gleichungen, der Magnetohydrodynamik oder den Navier-Stokes Gleichungen mit variabler Viskosität treten viele neue Effekte auf.
Inbesondere gibt es einen Wettbewerb zwischen stabilisierenden und destabilisierenden physikalischen Effekten.

Ein prototypisches Beispiel hierfür ist die Rayleigh-Benard Instabilität in den Boussinesq Gleichungen, welche eine wärmeleitende Flüssigkeit beschreiben:
$\partial_t v + v \cdot \nabla v - \nabla p = \theta e_2 + \nu \Delta v,$
$\partial_t \theta + v \cdot \nabla \theta = \kappa \Delta \theta,$
$\text{div}(v)=0.$
Hier haben wir einerseits einen destabilisierenden Effekt durch den Auftrieb heißer Flüssigkeit und anderseits Stabilisierung durch Dissipation und Durchmischung.

Als ein Hauptresultat und unserer Forschung konnten wir zeigen, dass diese nichtlinearen Instabilitäten durch die Interaktion von "wellen-artigen" Lösungen beschrieben werden können.
Insbesondere heben diese klar die Wechselwirkung zwischen den Effekten hervor und erlauben uns optimale Zeitskalen und Regularitätsklassen für (In)Stabilitätsresultate zu identifizieren.
Diese Interaktion zwischen Wellen, physikalischen Effekten und der Systemstruktur ist auch aktuelles Thema einer Dissertation zur Magnetohydrodynamik in der Forschungsgruppe.

Formgedächtnismaterialien sind Metalllegierungen die einen ersten Ordnungs Phasenübergang durchlaufen, von einer sehr symmetrischen Hochtemperaturphase (Austenit) zu einer Niedrigtemperaturphase (Martensit) mit einer weniger symmetrischen Struktur. Dieser Verlust von Symmetrie erlaubt viele verschiedene Martensit-Varianten. Daher sind Verformungen bei niedrigen Temperaturen energetisch relativ günstig und das Material kann leicht verformt werden. Beim Erhitzen werden jedoch alle Varianten wieder zur Austenit Phase und das Material nimmt wieder seine ursprüngliche Form an. Es hat ein "Gedächtnis".

Mathematisch werden diese Materialien variationell in einem Model von Ball-James beschrieben. Da das Variationsproblem stark nicht-konvex ist, ist die Existenz und Beschreibung von Minimierern ein sehr herausforderndes Problem. Für spannungsfreie Deformationen
$u: \Omega \rightarrow \mathbb{R}^n$
führt dies auf das differentielle Inklusionsproblem:
$\nabla u \in K.$
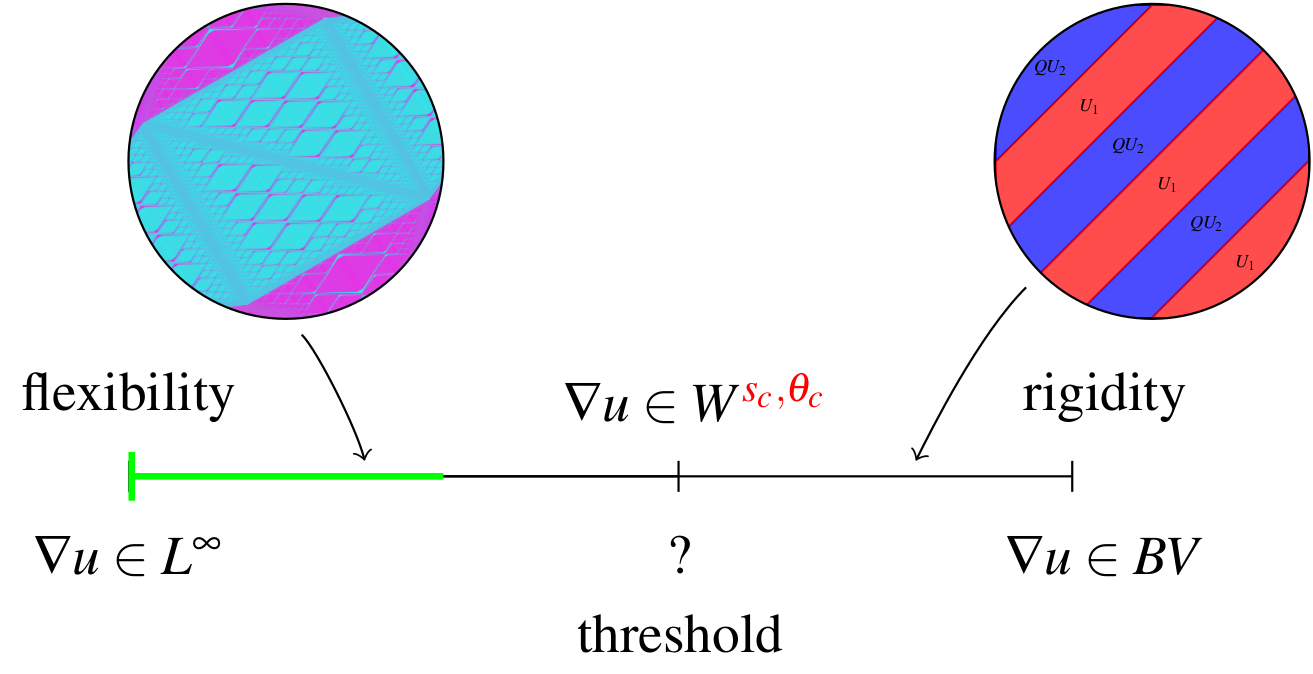
Bei vergleichsweise hoher Regularität ist dieses Problem "rigide": Lösungen können nur bestimmte Muster wie z.B. Streifen aufweisen.
Bei niedrigerer Regularität ist das Problem hingegen "flexibel": Es gibt unendlich viele "wilde Lösungen" mit sehr kompliziereten Mikrostrukturen.
Das Verständnis dieser Dichotomie zwischen Rigidität und Flexibilität und die Konstruktion wilder Lösungen in höherer Sobolev Regularität sind zentrale Forschungsziele der Gruppe.

Personen in der Nachwuchsgruppe
Name
PD Dr. Christian Zillinger

Aktuelles Lehrangebot
Semester	Titel	Typ
Wintersemester 2024/25	Klassische Methoden für partielle Differentialgleichungen	Vorlesung
Wintersemester 2023/24	Introduction to convex integration	Vorlesung
Wintersemester 2022/23	Introduction to convex integration	Vorlesung
Wintersemester 2021/22	Introduction to Kinetic Equations	Vorlesung
Wintersemester 2020/21	Seminar: Microstructure in materials and fluid dynamics	Seminar

Stability and Instability in Fluids and Materials

In our research we consider physically motivated problems in partial differential equations, which combine physical effects and interesting mathematical phenomena. Here a particular emphasis is on mixing, resonances and asymptotic stability in fluid systems with and without dissipation as well as rigidity and flexibility of convex integration in shape-memory alloys.

Mixing as a (de)stabilizing effect

Mixed

One of the major questions of fluid dynamics lies in the description of stability of fluids and their asymptotic behavior.
This analysis is of great interest due to the equations' mathematically challenging and intricate properties and also in view of their physical applications.

Here a central model is given by the incompressible Euler equations

$\partial_t v + v \cdot \nabla v - \nabla p = 0,$
$\text{div}(v)=0,$

where $v$ denotes the velocity of the fluid and $p$ is the pressure. Unlike the Navier-Stokes or Boltzmann equations these equations do not include common damping mechanisms such as dissipation or entropy increase. On the contrary the equations possess infinitely many conservation laws and are even time reversible.
Yet considering perturbations are shear flows $v=(U(y),0)$ one observes that small perturbations converge back to a shear flow as time tends to infinity, a phenomenon known as inviscid damping.
Mathematically this behavior can be described in terms of weak convergence and results in beneficial damping but also in deteriorating regularity due to the appearance of smaller and smaller mixing scales.
Moreover, the interaction and "un-mixing" of wave-like perturbations can lead to non-linear instability of the dynamics.

Resonance cascades in coupled fluid systems

Resonance cascades

New effects arise in coupled fluid systems such as the Boussinesq equations with partial dissipation, magnetohydrodynamics or the Navier-Stokes equations with variable viscosity. In all these systems there is an interaction of different, competing physical effects. A prototypical example is the presence of Rayleigh-Benard instabilities in the Boussinesq equations which couple thermal diffusion to the evolution of a fluid.
$\partial_t v + v \cdot \nabla v - \nabla p = \theta e_2 + \nu \Delta v,$
$\partial_t \theta + v \cdot \nabla \theta = \kappa \Delta \theta,$
$\text{div}(v)=0.$
Here there is a competition between the destabilizing effects of buoyancy on the one hand, and mixing-enhanced dissipation on the other hand.

As one of the main results of our recent research we show that non-linear instability mechanisms can be accurately captured in terms of the interaction of special non-linear, global in time solutions called traveling waves. In particular, this descriptions allows us to study the competition of these (de)stabilizing effects and identify associated time scales, norm inflation mechanisms and optimal spaces to prove regularity. This complex interaction of physical effects in coupled systems is also at the core of ongoing PhD work on resonances in magnetohydrodynamics within this research group.

Convex integration in materials

Shape-memory alloys are metal alloys which undergo a first-order diffusionless solid-solid phase transformation, passing from a highly symmetric high temperature phase (austenite) to a low temperature phase (martensite) with a less symmetric unit cell structure. This loss of symmetry gives rise to multiple variants of martensite. Hence, at low temperature deformations are energetically comparatively inexpensive, as different variants of martensite can accommodate macroscopic changes in shape. However, upon heating the material, all these variants are forced back into the austenite phase and thus the material recovers its shape. The material has a memory.

Mathematically, we describe these materials in terms of a variational model due to Ball-James. As this problem is highly non-convex the existence and description of minimizers is a very challenging problem.
Focusing on exactly stress-free states, we search for deformations
$u: \Omega \rightarrow \mathbb{R}^n$
which solve the differential inclusion problem
$\nabla u \in K.$
Here we observe that at relatively high regularity the equations are rigid: all solutions can only exhibit certain patterns.
In contrast, at lower regularity the equations are flexible and allow for infinitely many wild solutions with highly complex microstructures.
A main aim of our research is to develop a better understanding of this dichotomy between rigidity and flexibility and to construct wild solutions at higher Sobolev regularity.

Staff in the Junior Research Group
Name
PD Dr. Christian Zillinger

Current Offering of Courses
Semester	Titel	Typ
Winter Semester 2024/25	Klassische Methoden für partielle Differentialgleichungen	Lecture
Winter Semester 2023/24	Introduction to convex integration	Lecture
Winter Semester 2022/23	Introduction to convex integration	Lecture
Winter Semester 2021/22	Introduction to Kinetic Equations	Lecture
Winter Semester 2020/21	Seminar: Microstructure in materials and fluid dynamics	Seminar