Hydrodynamic (in-)stability of geophysical fluid flow

Vortices and vortex filaments

A fundamental question for the understanding of hydrodynamic stability consists in rigorously describing the dynamics of vortices and vortex filaments such as the propagation of vortex rings in inviscid or viscous fluids. The vortex filament conjecture states that initial concentration around such a curve persists and the curve evolves through the binormal curvature flow. In its generality, the conjecture remains unsolved and the evolution and interaction of vortex filaments in incompressible fluids remains a puzzling problem.
(Partial) answers are available if considered in specific geometric situations and dimension reduced settings. Vortex solutions are of low regularity and as such fall in general outside the usual well-posedness framework.
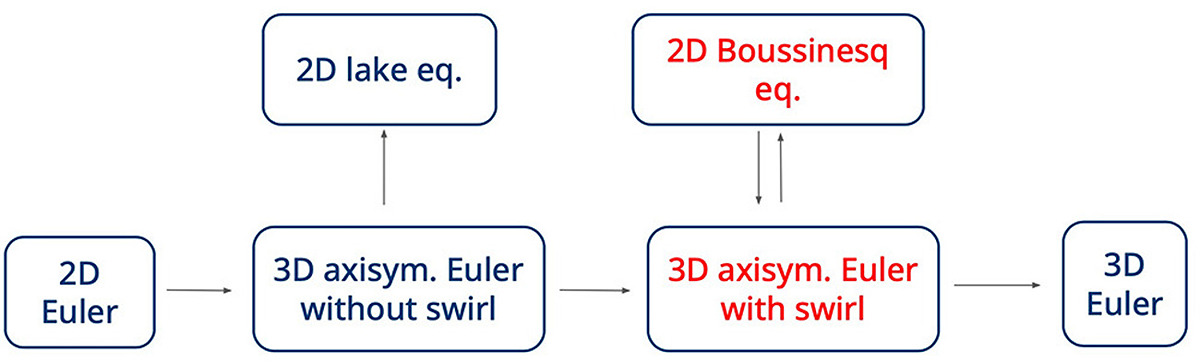
We derive and analyse the relevant asymptotic dynamics in contexts with spatial heterogeneities such as the (degenerate) lake equations describing a 2D fluid with prescribed but varying topography or the 3D axisymmetric Euler equations.

Specifically, we rigorously justify e.g. the vortex dynamics for the lake equations and the leapfrogging phenomenon in ideal incompessible fluid flow.

(In-)stabilities in geophysical fluid flow

A parallel research concerns ill-posedness phenomena and instabilities in models for geophysical fluid mechanics such as the (stratified) Boussinesq equations or the (degenerate) lake with rough geometries and topographies.
For the former for instance, we identify a nonlinear ill-posedness mechanism at critical regularity by a careful analysis of the interaction of nonlinear waves. The Boussinesq equations describing a non-homogeneous or stratified fluid are one of the models commonly used in oceanography and atmospheric sciences.

Beyond being of independent interest, the lake equations and 2D Boussinesq equations share strong mathematical analogies with the 3D axisymmetric incompressible Euler equations (the former without, the latter with swirl) which further motivates our study.

Back to the group Nachwuchsgruppe Vortices and Nonlinear Waves .